Here is a problem I found on Facebook. On the surface, it seems very challenging. I will admit it was a bit time-consuming. How did you feel upon seeing this? Did the many blanks horrify you? You can just imagine how a 4th grader might feel upon setting eyes on a long division problem for the first time.
However, I think that moments like that are a good time to model and teach critical thinking and persistence. I have seen students give up before they even started, because it "looked hard". It is important to show students that they can work through what looks so intimidating.
What took me a while was figuring out where to start. I decided to start by marking that the last 2 digits of the dividend are brought down in a typical long division problem.
Then I started working on the problem itself. I started by asking myself, "What would I need to multiply by 9 to get something that ends in 2?", for which the only answer is 8 (for a product of 72). I noted that I would need to add 7 to the product of 8 and the divisor's middle digit.
My next step was to think about what I could subtract from 8 (in the dividend) to get a difference of 9. This of course means that I would have had to borrow from the digit in the ten thousands place to turn 8 into 18. The missing number is therefore 9.
Then, having found out that the digit directly under 8 is 9, I started thinking about what I needed to multiply by 8 and then add 7 to, to get something that ends with 9. My choices at this point were 4 (4•8=32; 32+9=39) and 9 (9•8=72; 72+9=79). With no way of knowing, I decided to use trial and error, and try 4. I noted that I would have to add the 3 (from 39) to the leftmost digit of the divisor.
To find out what the leftmost digit in the divisor is, I thought about what I can multiply by 8, and then add 3 to, to get something less than (or possibly a little bit greater than) 60. I tried 7, because 8•7=56, and 56+3=59.
Then I had a moment of insight. I looked at the bottom of the problem and realized that there is no remainder for this problem. This meant that there had to be a 4 under the 4, to get a difference of zero.
After that, I multiplied my potential divisor by the 5 in the quotient, and plugged the product in.
I noticed that I had a 9 in the first difference, with a 7 directly beneath it, meaning there was a difference of 2 to be written down.
I also multiplied the divisor by the last digit (3) of the quotient and wrote the product down. Because there is no remainder, I copied the product onto the line above as well. I found out what the digit in the dividend's ones place was (7), and copied it up to the dividend.
It was then time to work backwards. Instead of subtracting, I added, to fill in the upper blanks. In this way, I was able to determine that the digit in the tens place in the dividend was a 9.
I continued working backwards, adding instead of subtracting. I remembered that I borrowed from the digit in the ten thousands place to turn 8 into 18, so I made sure to add that 1 back in.
I checked my work, as a matter of habit, by multiplying the quotient by the divisor. If I did it correctly, I would arrive at the dividend that I came up with.
Et voila! Success! Did I absolutely have to solve a math problem that I found on social media? No. What possessed me to do so? It was a challenge, and I didn't know if I could solve it. I wanted to know for sure, so I tried it. Would I have given up if I had guessed wrong on the 2 missing digits in the divisor? No. This is where the importance of teaching persistence comes in. Some students are prone to giving up after making a mistake, convincing themselves that the problem was too hard anyway, and it wasn't a surprise that they failed.
Backtracking is not a popular idea with students, not only in math but in other processes as well. I taught origami after school, and I can attest that my students' least favorite step is unfolding. They never like the idea of doing something and then undoing it. It is a hard concept to grasp, using the mark they made as a basis for something else or something more. In math, when that error is made, students need to see it as a step in the right direction. It is not only the point at which they made a mistake; it is also the point where they found out what path not to take. Eliminating a choice, in math, is progress.
I posted my answers as a comment to that image on Facebook, and then someone sent me a private message, asking me how I figured it out. I then had to think about the best way to explain my thinking. It was slightly intimidating, honestly, mainly because I wasn't thinking about my thought process when I solved it. Writing it all down would have been tedious. I made a video, but I did not speak because I had a problem with hearing my own recorded voice.
The video is shown below. I hope that if my explanation above wasn't too helpful, the video below will clarify the steps I took.














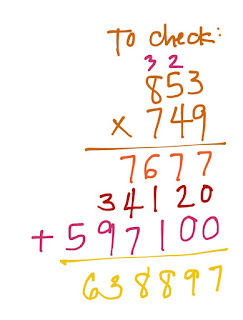
No comments:
Post a Comment