IT'S ALL MATH AND GAMES

I love math. I understand that there are not a lot of people who feel the same way. I think math is fun. I know that that concept is hard for others to grasp. I can make math fun. I have made math fun. 

In my previous post, I talked about attending the TIES conference in 2014. It was a very eye-opening experience. One of the things I learned about was coding. I learned about Scratch. I learned to code. I learned to make a few math games for practice, and one for assessment of multiplication fluency. I understand that not everyone will be motivated to learn a little bit of coding to do what I did, so I am sharing what I have made. If you find them useful, great. If not, think about how you can make it better. It is okay to "remix" someone else's work in Scratch.

Multiplication Fact Fluency with DCPM (Digits Correct Per Minute): This game requires 5th graders to achieve or surpass 36 DCPM, and 4th graders to get at least 28 DCPM.

Exploding Dragon Games (addition, subtraction, multiplication, and division, with immediate feedback): This shows the correct answer if a student answers incorrectly.

I also have games for rewards (addition, subtraction, multiplication, and division). Again, you can remix these to fit whatever reward you are offering. A "caught you" is a piece of paper given to students who are "caught being exceptional"; these pieces of paper are placed in a classroom raffle, and winners get to pick a prize in the principal's office on Fridays. I used these games in child care during parent-teacher conferences. I have actually made it a given that I work in child care during conferences, and I have math games and prizes. I recommend telling students to play for at least 3 minutes, but no more than 5.

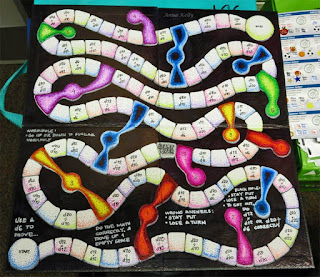
As a math tutor, I also created a couple of board games for my students to play. I ended up having 4th and 5th graders reserving recess time to come in and play games (even in nice weather). The first one is modeled after chutes and ladders, except I had snakes instead of chutes. If they landed on a "Draw a Card" spot, they had to do math. Wrong answers meant losing a turn, correct answers moved them forward to a specified spot on the board. I like to tell students that I have gone down the big snake twice in one game, just so they don't feel defeated after being "eaten".

My second game is more difficult, and therefore less popular. It is called blackholes and wormholes. I used different dice within the game: 6-, 10-, 12-, and 20-sided. On the board, there are different operations to be carried out, if a player lands on certain spots. For example, if it said d20÷d20, they had to roll 2 20-sided dice and divide the bigger number by the smaller number to get the quotient and the remainder. If they answer correctly, they move to the next empty space. Colorful wormholes moved teleported them up or down to the wormhole of a matching color. Blackholes meant they lose a turn and have choices as to how to get out on their next turn. While not as popular, this game was preferred by my more advanced students, because it was more challenging.

I am aware that teachers do not always have time to create their own teaching materials. I will admit that each of these board games took over 6 hours to finish. However, I do encourage teachers to find fun ways to teach math and practice skills, especially if there are students who will most likely be more engaged when games are used.

GAMIFIED INSTRUCTION

What on earth is "gamified instruction"? Does it mean using games to teach a lesson? Well, yes and no, but mostly no. I learned about gamification when I attended the TIES conference in December 2014. In the school year 2013-2014, my tutoring students were engaged enough. We were making progress. Some of them were skipping whole lessons or even units based on pretest results. We did not need any help.

However, on my second year of tutoring, they changed the curriculum drastically. There were no more pretests and no opportunity to skip the lessons that students already were proficient in. There were more assessments. We were given a script to follow in teaching the lesson. It had become more rigid and more boring. If there is one thing that math doesn't need to become, it's more boring. So after attending the TIES conference, I decided to change up my tutoring sessions. I technically could not change any part of the curriculum, but no one said I can't make the whole process fun.

I wrote about the first few weeks, and uploaded a PDF to my TeachersPayTeachers.com account. Feel free to download a copy here. You will need to have an account to download it. It costs nothing to create an account or download my PDF.

Gamified instruction does not mean that you are including games in your instruction; it means that the whole instruction process becomes a game of some sort. In a nutshell, I allowed my students to create an avatar/logo, an alter ego name and a (useless) superpower. In an effort to maintain anonymity for those who wanted to stay anonymous, I typed up their names and superpowers. In the photo below, you can see some of my students' avatars on top and their superhero names and powers in the bottom of a long strip of paper. In the middle of the strip are their badges. For every lesson finished they earned a badge to put up on their strip. I taught in pairs, so for some students, only their partners are aware of which strip is theirs. I found it necessary to offer secrecy to those who were not confident of their skills or afraid of being judged by others because of their lack of progress.

I did spend a great chunk of my winter break creating the badges. I knew that it was possible to create badges the easy way through Credly, Schoology (especially if you're already using it anyway), Badge Maker, and other badge-making websites. However, even before we started, I had one student ask me, "What if I found the badges online and printed them out myself?" I found this question very unsettling, although I was not at all surprised that this student asked that question. I told her I was going to make it from scratch, which I did, using IconMaker for Mac. The badges I created are shown below:

Most of them were lesson-related. Some were to encourage students to save up their reward cards for more significant prizes. A few were to acknowledge that they finished the monthly STAR assessment they needed to go through in addition to the 1-3 assessments after every lesson. 

Because "assessment" has become a negative term, I called our assessments "quests". Our lessons were effectively practicing for the quests. Their scores in quests became XP points for leveling up. If they fail a quest, they'll have to use another life to try it again after more training. The change from "assessment" to "quest" resulted in a great change in attitude. We needed to repeat "quests" very few times, and all of a sudden, it mattered to get the best score possible, not just pass or survive.

It can be challenging to have students who have the mindset that they are just not good at math. I highly recommend taking the time to gamify instruction, if it will help students get engaged. Sometimes we just have to give the students something to be enthusiastic about.

I am thankful for having had the chance to listen to Jane McGonigal speak. Here is her TedTalk about gaming. If you don't want to watch the whole thing, at least skip to 3:25 and listen to the next minute or less about what is significantly different about how problems are tackled in games and in real life. This is why I gamified my teaching.

MULTIPLICATION MATTERS

I learned my multiplication table virtually overnight, when I was in 3rd grade. I had this math teacher who had long nails. She liked to randomly call on students and, if they were not able to answer correctly, she poked them on the head with those nails while saying, "Study, study, study". I didn't want to be poked on the head. My wild imagination led me to believe she was going to draw blood (although to my knowledge, she never did). I memorized the table so I can make sure that I never got poked on the head; it worked.

Fast forward three decades...I was dealing with 4th and 5th graders who could not memorize their math facts, for one reason or another. I still encounter students who just cannot remember. I wish I had a tip for them, for memorizing their facts. I certainly would not wish them to learn out of fear like I did, but I am at a loss as to how to help them memorize. If those catchy rhymes like "Six times eight I used to hate, now I know it's forty-eight" don't work, what will?

I decided not to focus on memorization. Rather, I thought I would teach students how to figure it out. If they can't memorize, they should at least know how to get there without counting up all the way from one.

I used to have this multiplication table hanging in my room when I was a tutor. My students asked why I didn't write all the products down. I said it wasn't my job to give them all the answers. I just needed to help them know how to figure things out themselves.

So, when a student cannot remember what 6•7 is, I teach them to go back to what they know (and I assume they know the multiples of 5 and 10). Typically, it means going back to 5•7. So I ask, "If you have 5 sevens, you have...?" and they answer 35. Then I ask, "If 5 sevens is 35, what would 6 sevens be?" and sometimes I have to word it differently, like "If 5 sevens is 35, 6 sevens would be 7 more than 35" if the student is truly struggling.

Sometimes it's multiples of 9 that gives them trouble. I try to remind them of the "finger trick" but even that can be hard to remember. So if a student is trying to solve 9•8, I guide them by asking, "Would you like to start at 5•8 or 10•8?" If they had worked with me before, they would know to start from 10•8 and work their way down. 

This is not ideal. It takes time, but it takes less time than counting up from one (and possibly losing count)...or drawing 72 dots on paper. Of course, one would hope that with as many times as we go through it, some of the facts will stick. Until that happens, and because it is futile to get frustrated over what is not being memorized, the least we can do is provide the students with a better understanding of number sense so that they can work out what they cannot memorize. That's one more tool in their virtual toolbox.

THE DAY I TAUGHT A LESSON: HOW RELATIONSHIPS AFFECT MATH

(Click on the image above to access the slideshow mentioned in this post.)

Sometimes we have the best intentions and what we think are the best strategies, and then we end up having some doubts about them. As a math tutor a few years ago, I was given a tip that I thought I would try. Veteran tutors said that if I made word problems with my students' names and interests, they would be more invested in their learning. I did this for the 2 years I taught; I also allowed my students to write their own word problems, for as long as they related to the current lesson. They came up with interesting stories where their tutoring partner inevitably got hurt, for example, by tripping and falling down so many feet down the mountain.

For the lesson I taught in my mentor's classroom, I thought I would do the same. The students were very engaged, which I expected. They especially enjoyed it when the story had them doing something they would not do in real life, like share their pencils.

When we got to slide 9, where they all needed to get in canoes that held 3 persons each, they inevitably added their teacher to the count, even if the problem did not say she was part of it. They logically assumed that if the class was going on a trip, that she would be there as well. However, I reminded them to focus on the problem itself, and not to embellish the story. While it did not affect the final answer, it needed to be brought to their attention.

We again encountered the problem on slide 12, where half of the class assumed that Geo would share his money with Osvaldo. I had the students work on this problem independently and hold up their whiteboards to share their answers. As soon as everyone got a look at everyone else's answers, discussions ensued. I brought it to order and asked a representative from each side to explain their thinking. I started with the students who said that, yes, Osvaldo can afford to buy the tacos. Then I asked someone who answered no about how they came up with a different answer. All the students who answered yes assumed that Geo would share his money. I found it necessary to ask where in the problem it stated that Geo did that. I had to point out again that they cannot add to the story given to them.

It was hours after the lesson that I started thinking about how relationships within the classroom could have affected the outcomes. I started wondering if the outcomes would have been different if the names weren't familiar. If I hadn't used their teacher's name, would they have thought to include the teacher in the count? If I didn't pick the names of 2 students who were friends, would they have assumed that the second person would be so generous? Did I skew the results by getting them too engaged in the lesson? Is there such a thing as being too engaged in a lesson? Hmmm.

THE DAY I TAUGHT A LESSON: WHAT WORDS MEAN

On the 12th of October, I taught a lesson in my mentor's classroom. Because my lunch break coincided with math instruction in her classroom, I taught a math lesson. I taught a lesson in breaking down word problems to understand what needs to be done.

As I was planning this lesson, I looked back to Mr. Popper's Penguins and using words as labels for variables. I knew that even if that website was geared towards 2nd graders, I could use that strategy with struggling 5th graders.

Click on the image above to access the slideshow I used to teach my lesson. Apart from using words to label variables, I also emphasized that words have the power to change what the answer is. 

In slide 5, when I asked for keywords, I got "sum" and "and". I told them that "is" is equivalent to an equal sign. I told them that "What" is also a keyword, and I was asked why. I answered by way of giving examples. I asked, "What are the answers to the question 'Are you eating right now?'?" and they said "Yes or no". I asked them if they still would answer yes or no if the question was "What are you eating right now?", and it became clear.

As we continued with the lesson, we had more opportunities to analyze the questions that are asked. My students tended to know what needed to be done mathematically, and automatically assume that the answers to the questions were numbers. I emphasized reading the question twice. For example, in slide 8, it asked, "Does she have enough money?", to which the answer is either yes or no.

The last slide was tricky, and it was meant to be tricky. I did not intend for it to be an assessment of my students' skills. Rather, it was meant to increase awareness of how we all tend to assume that we know what is being asked. We tend to focus on certain words and not others. My students saw the word "volume" and assumed that they knew what to answer. However, the question was not about the "volume of the hole", but rather the "volume of dirt in the hole". My husband got it wrong, too. How about you?

THE IMPORTANCE OF CRITICAL THINKING AND PERSISTENCE

Here is a problem I found on Facebook. On the surface, it seems very challenging. I will admit it was a bit time-consuming. How did you feel upon seeing this? Did the many blanks horrify you? You can just imagine how a 4th grader might feel upon setting eyes on a long division problem for the first time. 

However, I think that moments like that are a good time to model and teach critical thinking and persistence. I have seen students give up before they even started, because it "looked hard". It is important to show students that they can work through what looks so intimidating.

What took me a while was figuring out where to start. I decided to start by marking that the last 2 digits of the dividend are brought down in a typical long division problem. 

Then I started working on the problem itself. I started by asking myself, "What would I need to multiply by 9 to get something that ends in 2?", for which the only answer is 8 (for a product of 72). I noted that I would need to add 7 to the product of 8 and the divisor's middle digit.

My next step was to think about what I could subtract from 8 (in the dividend) to get a difference of 9. This of course means that I would have had to borrow from the digit in the ten thousands place to turn 8 into 18. The missing number is therefore 9.

Then, having found out that the digit directly under 8 is 9, I started thinking about what I needed to multiply by 8 and then add 7 to, to get something that ends with 9. My choices at this point were 4 (4•8=32; 32+9=39) and 9 (9•8=72; 72+9=79). With no way of knowing, I decided to use trial and error, and try 4. I noted that I would have to add the 3 (from 39) to the leftmost digit of the divisor.

To find out what the leftmost digit in the divisor is, I thought about what I can multiply by 8, and then add 3 to, to get something less than (or possibly a little bit greater than) 60. I tried 7, because 8•7=56, and 56+3=59.

Then I had a moment of insight. I looked at the bottom of the problem and realized that there is no remainder for this problem. This meant that there had to be a 4 under the 4, to get a difference of zero.

After that, I multiplied my potential divisor by the 5 in the quotient, and plugged the product in.

I noticed that I had a 9 in the first difference, with a 7 directly beneath it, meaning there was a difference of 2 to be written down.

I also multiplied the divisor by the last digit (3) of the quotient and wrote the product down. Because there is no remainder, I copied the product onto the line above as well. I found out what the digit in the dividend's ones place was (7), and copied it up to the dividend.

It was then time to work backwards. Instead of subtracting, I added, to fill in the upper blanks. In this way, I was able to determine that the digit in the tens place in the dividend was a 9.

I continued working backwards, adding instead of subtracting. I remembered that I borrowed from the digit in the ten thousands place to turn 8 into 18, so I made sure to add that 1 back in.

I checked my work, as a matter of habit, by multiplying the quotient by the divisor. If I did it correctly, I would arrive at the dividend that I came up with.

Et voila! Success! Did I absolutely have to solve a math problem that I found on social media? No. What possessed me to do so? It was a challenge, and I didn't know if I could solve it. I wanted to know for sure, so I tried it. Would I have given up if I had guessed wrong on the 2 missing digits in the divisor? No. This is where the importance of teaching persistence comes in. Some students are prone to giving up after making a mistake, convincing themselves that the problem was too hard anyway, and it wasn't a surprise that they failed.

Backtracking is not a popular idea with students, not only in math but in other processes as well. I taught origami after school, and I can attest that my students' least favorite step is unfolding. They never like the idea of doing something and then undoing it. It is a hard concept to grasp, using the mark they made as a basis for something else or something more. In math, when that error is made, students need to see it as a step in the right direction. It is not only the point at which they made a mistake; it is also the point where they found out what path not to take. Eliminating a choice, in math, is progress. 

I posted my answers as a comment to that image on Facebook, and then someone sent me a private message, asking me how I figured it out. I then had to think about the best way to explain my thinking. It was slightly intimidating, honestly, mainly because I wasn't thinking about my thought process when I solved it. Writing it all down would have been tedious. I made a video, but I did not speak because I had a problem with hearing my own recorded voice.

The video is shown below. I hope that if my explanation above wasn't too helpful, the video below will clarify the steps I took.

BUT IS THIS REALLY THE PROBLEM WE NEED TO SOLVE?

If you were like me, you would have solved this the moment you saw it. If you’re not like me, you probably scrolled down to see the comments that people left on the Science Channel’s post sharing this problem (and the solution). Below is a screenshot of a few of the answers given by Facebook users. (Hint: Click on the image above to go to the video explaining how to go about solving it. Click on the image below to go to Science Channel's Facebook post.)

This is the type of thing that infuriates and saddens me at the same time. This is why I decided to become a math tutor, and why I was a math tutor for two years. This affected me so much that I even mentioned it in my interview for that position. I was asked why I wanted to become a math tutor, and I said, I would like to help students master the basic mathematical ideas taught in grade school and retain their knowledge for years to come. I wanted fewer wrong answers, and fewer arguments in defense of wrong answers.

            I wanted children to see math as something they will need all their lives, not just something to “survive” in school and then forget promptly after graduation. I wanted children to realize that math can be fun, and I wanted to be that person who made it fun. I would like to think that I did just that. It wasn’t easy; there were too many students who had the “I’m not good at math” mindset. There had to be extrinsic rewards they can earn; there had to be that chance of saving up rewards cards for Jolly Rancher cotton candy.

            Did it work? It seemed like it did. I can’t count the times we spent the tutoring session making and eating cotton candy, which cost the student 4 reward cards, each with 10 punch slots. So that’s 40 punched or stamped slots for cotton candy. How much work did they have to do for cotton candy? I gave them 1 stamp for every half hour they were with me, and they spent at least 90 minutes a week with me. That means 3 stamps if they were present all week. At the end of the week, I had 2 math questions they could solve for an extra stamp each; it was a choice, but they all seemed to want to do the work. One of the questions always was about order of operations…always. The other was based on whatever was being taught in class at any given point in time. So if they were present all week, and solved the problems I gave them, they got 5 stamps each week. How many times does 5 go into 40, or what is the minimum number of weeks it took them to earn cotton candy? The answer is 8 weeks. Right now, you’re thinking, that Jolly Rancher cotton candy must have been good. It was.

            Do you know what’s even better? We just did some math.